The Kullback test does something pretty simple: it shows you at what distance a string of text starts to repeat on itself. For instance, the test would tell you that the string xyzxyzxyzxyzxyzxyzxyzxyzxyz repeats itself in distances of 3. Although this test is mostly used to defeat polyalphabetic ciphers like Vigenere, I think this test can be extended to (non-vigenere) CTF crypto challenges. This post is basically me trying to convince you that it’s something worthy to add to your toolbelt. At the end of this post, I’ll show off the test being used in a bunch of different situations, ending off with how it helped me in an actual CTF challenge.

Creating the Kullback Test

This part explains the process of how to implement the test. If you don’t care about that and just want the code/examples of using it, scroll down to the “Using the Kullback Test” section. To implement it, we need to write code doing the following:

For n in a given range (1 to 60 is fair):

• Transpose data into n blocks
• Score how random these blocks are on average (done with the index of coincidence)
• Store this value

Then, graph these stored values.

That might not make sense. Don’t worry, I’ll explain the points a little better downwards. Continuing on, here’s Python pseudocode of what our code should generally look like:

from statistics import mean # calculates mean of data
text = "xyzxyzxyzxyzxyzxyzxyzxyzxyz"
iocs = []

def transpose(txt,n):
	# code to transpose data into n blocks
	# returns a list of size n containing the transposed blocks
def ioc(txt):
	# code to calculate the index of coincidnce of a given text

for n in range(1,60): # i know this doesn't include 60 shut up
	transpositions = tranpose(text,n)
	avgioc = mean([ioc(x) for x in transpositions])
	iocs.append(avgioc)
	
plot(iocs) # replace with a bunch of code to plot the iocs array

With this in mind, let’s get to filling out our functions and the rest of the code!

Writing transpose(text,n)

By ‘Transpose data into n blocks’ I mean to split the text into multiple chunks of length n, layer them ontop of eachother, and read this stack of text by columns. For instance, here’s what should happen if you call transpose("xyzxyzxyzxyz",3): You can write this however you’d like. Here’s my solution:

def transpose(txt,n):
    transposed = ["" for _ in range(n)] # creates list of n empty strings
    for i, c in enumerate(txt):
        transposed[i % n] += c
    return transposed

Writing ioc(txt)

The IOC or Index of Coincidence is a fancy way to calculate the randomness of some given text. This is done by calculating how many times each letter shows up relative to the length of the text. The index of coincidence formula is as follows: 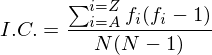That might look a little scary, but it’s really not that bad. This is saying:

• Grab how many times each character in the ciphertext shows up, aka its frequency
• For every character, calculate frequency*(frequency-1). Sum all the resulting values.
• Divide this sum by length*(length-1) (where length is the length of the given text)

Here’s my solution:

from collections import Counter

def ioc(txt):
    counts = list(Counter(txt).values()) # Counter(txt) returns a dictionary of all characters and their frequencies
    numerator = sum([x*(x-1) for x in counts])
    return numerator/(len(txt)*(len(txt)-1))

Plotting all IOCs

Repeating our Python pseudocode:

from statistics import mean # calculates mean of data
text = "xyzxyzxyzxyzxyzxyzxyzxyzxyz"
iocs = []

def transpose(txt,n):
	# code to transpose data into n blocks
def ioc(txt):
	# code to calculate the index of coincidnce of a given text

for n in range(1,60): # i know this doesn't include 60 shut up
	transpositions = tranpose(text,n)
	avgioc = mean([ioc(x) for x in transpositions])
	iocs.append(avgioc)
	
plot(iocs)

We just made transpose(txt,n) and ioc(txt). Now we just need to plot our data! We can use the matplotlib library to do this, and get our final (much more messy) code:

text = r"""xyzxyzxyzxyzxyzxyzxyzxyzxyz"""

remove = '' # characters matching this regex will be removed from the input text
casesensitive = True # if your text isn't case sensitive
maxtest = 60 # max keylength to try if it can be tried
threshold = .85 # probably no need to change this, threshold at what points should be annotated

from collections import Counter # to count frequency of every character
import matplotlib.pyplot as plt # graph plotting
from statistics import mean, stdev # to calculate the mean/stdev, not needed but it makes it more readable
import re, itertools # cleaning up input text


def ioc(txt): # calculate index of coincidence of given text
    counts = list(Counter(txt).values()) # Counter(txt) returns a dictionary of all characters and their frequencies
    numerator = sum([x*(x-1) for x in counts])
    return numerator/(len(txt)*(len(txt)-1))

def transpose(txt,n):
    transposed = ["" for _ in range(n)] # creates list of r empty strings
    for i, c in enumerate(txt):
        transposed[i % n] += c
    return transposed
    
def cluster(data, maxgap): # this isn't needed for the test, this is solely to graph the data better. stolen from https://stackoverflow.com/questions/14783947/grouping-clustering-numbers-in-python
    groups = [[data[0]]]
    for x in data[1:]:
        if abs(x - groups[-1][-1]) <= maxgap:
            groups[-1].append(x)
        else:
            groups.append([x])
    return groups
    
def check(input,rnge): # run kullback text up to a given range
    if not casesensitive: # uppercase text
	    input = input.upper()
    input = re.sub(remove,'',input) # removing unneeded characters
    print(input)
    xc, yc = list(range(1, rnge)), [] # xcoordinates, ycoordinates
    for x in range(1,rnge): # calculate IOC for each transposition length
        transpositions = transpose(input,x)
        avgioc = mean([ioc(y) for y in transpositions])
        yc.append(avgioc)
    plt.plot(xc,yc,'-bD',mfc="red") # plot points
    # code to label datapoints if the datapoint is above the average ioc for the text
    plt.ylim(top=max(yc)*1.05)
    iocmean = mean(yc)
    iocstdv = stdev(yc)
    spikes = []
    for i in range(rnge-1):
        if(((yc[i]-iocmean)/iocstdv) > threshold): # if the point deviates from the mean, treat it as a spike
            spikes.append(i)
    # removing clusters of spikes
    for k in cluster(spikes,1):
        m = max([yc[i] for i in k])
        # annotating (adding the number) above any spikes)
        plt.annotate(yc.index(m)+1,xy=(yc.index(m)+1,m),size=20,weight='bold',va="bottom",ha="center")
    plt.show()
    
check(text,min(int(len(text)/2)-1,maxtest))

Using the Kullback Test

The code is right above if you want to steal it. Here’s the Kullback test being used in a bunch of different scenarios, lastly a recent PicoCTF challenge.

Breaking Vigenere (and why the test works)

Let’s start off with using the test in its most common situation. If you have text enciphered with vigenere and you know the length of the key used, you can transpose the text into keylength blocks and break each block like a Caesar cipher (which is very easy to break*). If you can’t visualize how that works, let’s encipher a repeating single letter with the vigenere cipher in CyberChef: As we can see, every third letter from the start is f. That’s because each one was enciphered with the same letter in the key, b! If we provide the output to our program’s transpose() function with n as 3 (the length of the key):

def transpose(txt,n):
    transposed = ["" for _ in range(n)] # creates list of r empty strings
    for i, c in enumerate(txt):
        transposed[i % n] += c
    return transposed
text = "fghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfgh"
print(transpose(text,3))

# OUTPUT:
# ['fffffffffffffffffffffffffffffffff', 'ggggggggggggggggggggggggggggggggg', 'hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh']

Each list is a single letter, just like our input. That’s because we extracted the parts of the text enciphered by the same letter in the key! We can treat each string as a Caesar cipher, undo our transposition, and get our plaintext back!

Of course, we have to find this keylength ourselves from just the ciphertext. Our test does exactly that! We try every transposition up to a limit and check if the output lists are random. Since each string in the list is a single letter when transposed into 3 groups, the IOC test will mark each string as highly non-random and give it a very high score. If we plug our text into the entire program, we get an output graph like so: 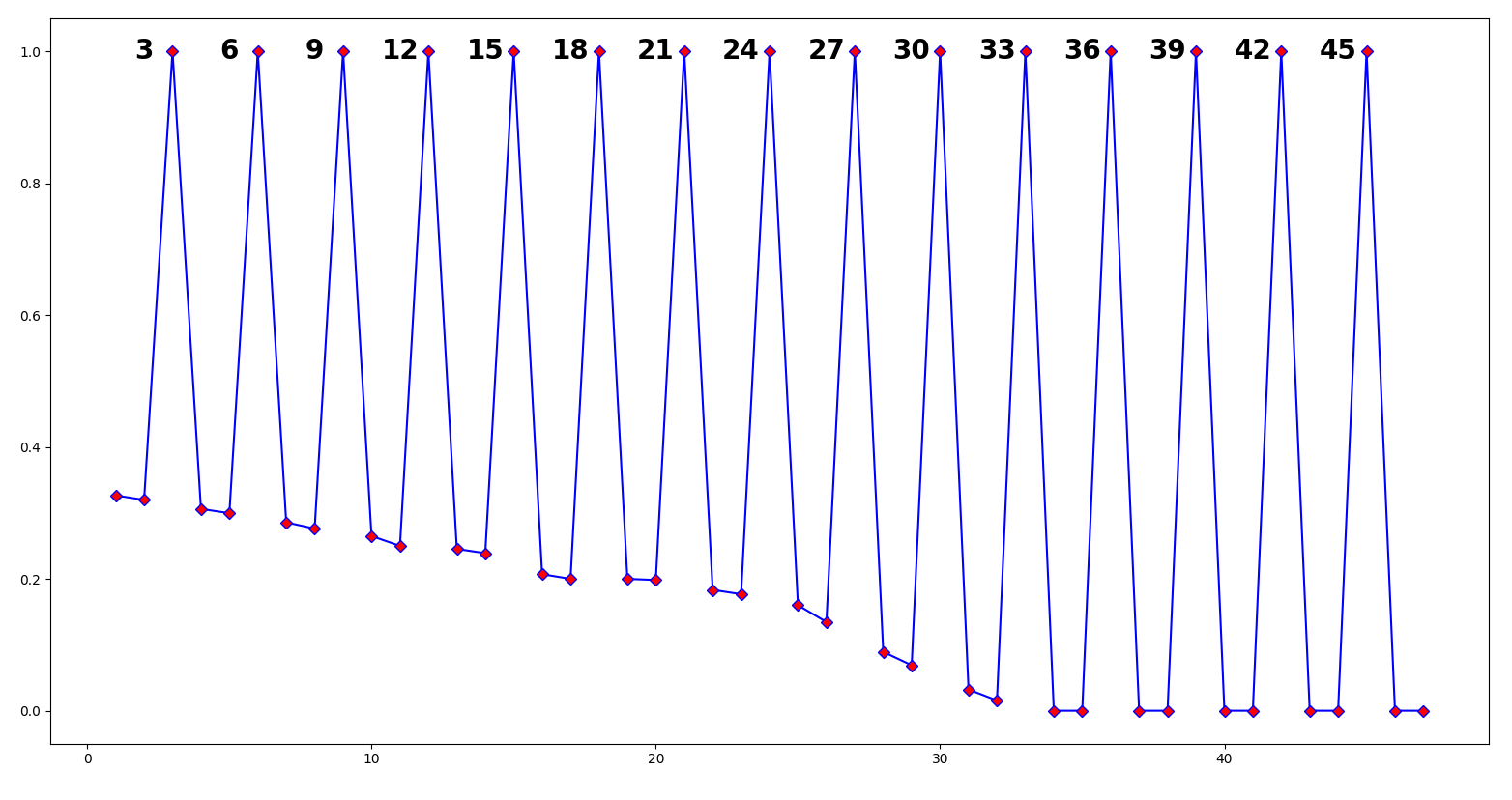We get constant spikes in the data in intervals of 3, our keylength! This is because if we transpose the text in intervals of 3n (3, 6, 9, 12..) we get the same repeating single-letters in each list, meaning the IOC will spike:

def transpose(txt,n):
    transposed = ["" for _ in range(n)] # creates list of r empty strings
    for i, c in enumerate(txt):
        transposed[i % n] += c
    return transposed
text = "fghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfghfgh"
print(transpose(text,3))
print(transpose(text,6))
print(transpose(text,9))
print(transpose(text,12))

# OUTPUT:
# ['fffffffffffffffffffffffffffffffff', 'ggggggggggggggggggggggggggggggggg', 'hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh']

# ['fffffffffffffffff', 'ggggggggggggggggg', 'hhhhhhhhhhhhhhhhh', 'ffffffffffffffff', 'gggggggggggggggg', 'hhhhhhhhhhhhhhhh']

# ['fffffffffff', 'ggggggggggg', 'hhhhhhhhhhh', 'fffffffffff', 'ggggggggggg', 'hhhhhhhhhhh', 'fffffffffff', 'ggggggggggg', 'hhhhhhhhhhh']

# ['fffffffff', 'ggggggggg', 'hhhhhhhhh', 'ffffffff', 'gggggggg', 'hhhhhhhh', 'ffffffff', 'gggggggg', 'hhhhhhhh', 'ffffffff', 'gggggggg', 'hhhhhhhh']

An alternative way to look at why this happens is that the vigenere key bcdbcd is equivalent to bcd. And so is bcdbcdbcd, and bcdbcdbcdbcd… Of course, we’re testing ciphertext against a single repeating letter e, and not real text. But if you think about it, English text is just the letter e with a bunch of noise around it… Here’s the test against 150 letters of text encrypted with the key virginia: 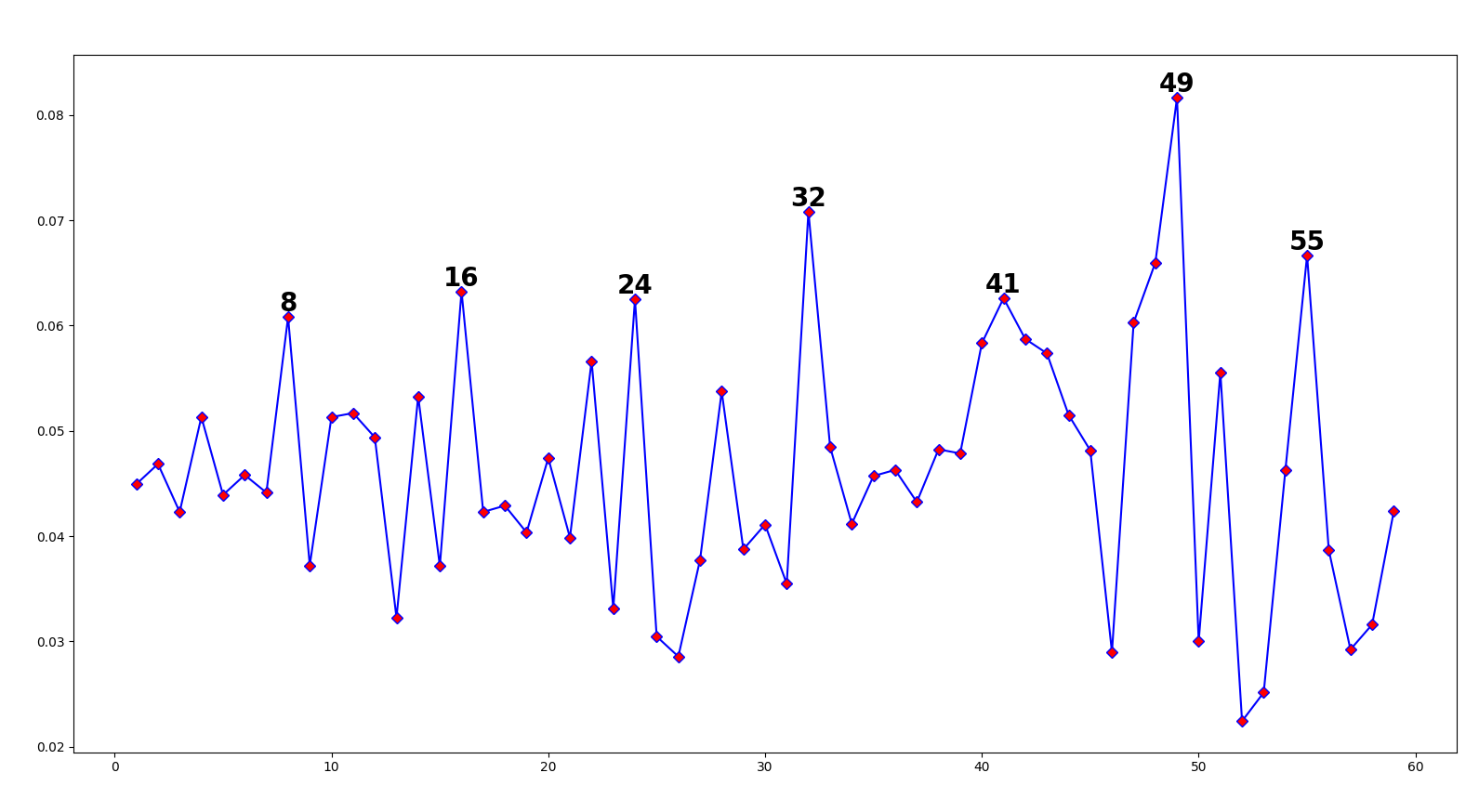The periodic spikes trail off after 32, but there are still consistent spikes in intervals of 8 (our keylength). And if we try the test against a greater sample of text, the noise disappears:

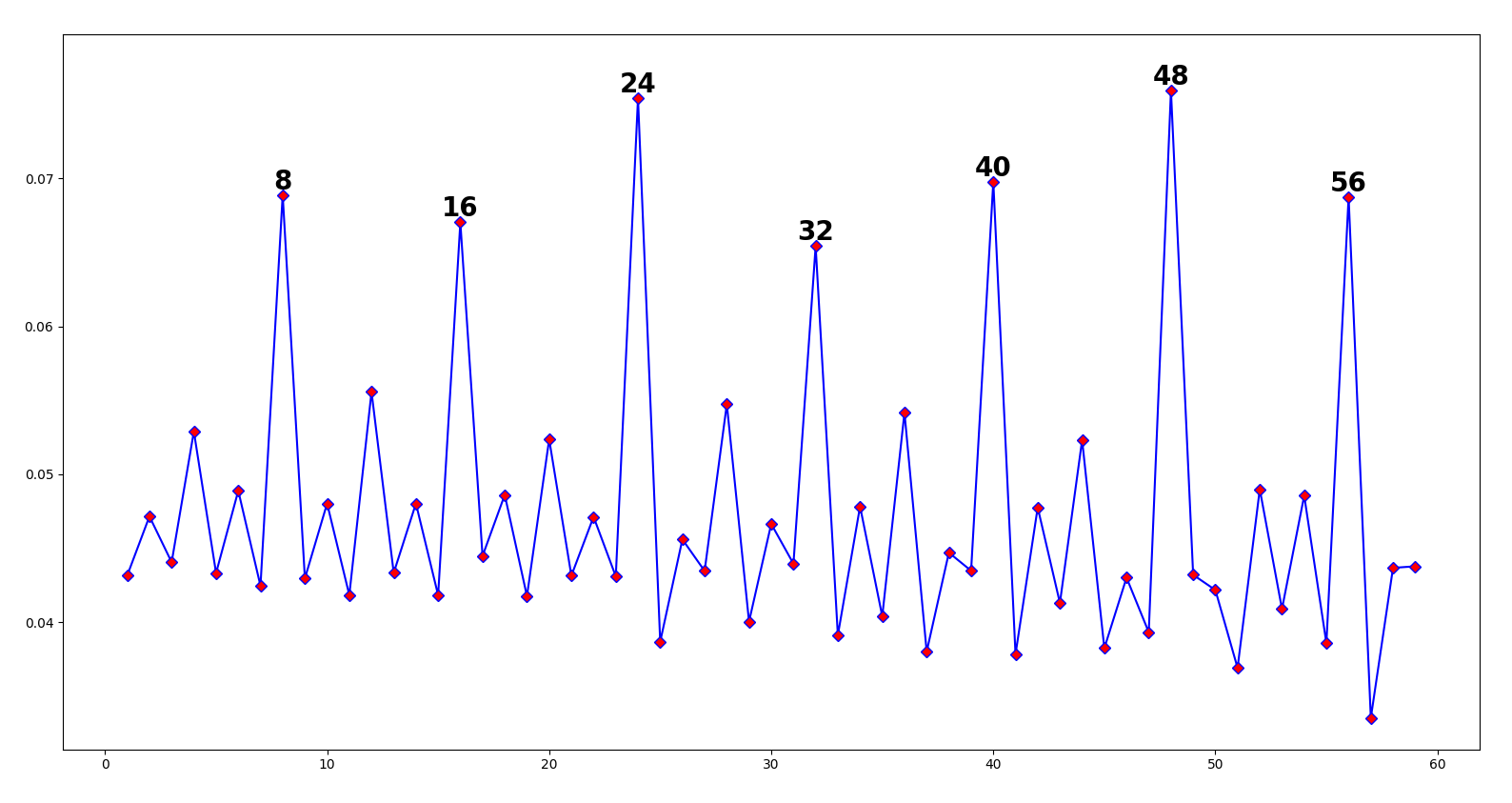
Breaking a custom cipher

The Kullback test can do more than just break Vigenere! Here’s a fairly simple cipher I made that the Kullback test can help defeat:

4701020602796294064080016287267947400699625688014740026880263322886831620268800140226268404756402668065662684002803362012268889567884002674701335680019440904706944022688895023762568040629562010267626822886895800126626768624062010262940601023706406287260602060105268879798056886880020688015662023162620131620268800140226268226888950237625680406295620102800194408801884068809406888801226256684780689840904706946862796280406294800162317998686226886894629499626840068801882202376202688026338040804006010579626862020602796294403106010506018094686280958037628094882202376268627962804062882202376206688079564795889588018879060237880134470162990680318068676862268868944037628094880188996268028831626768624062010202886862809480016287267947400699620601026268990662313106023740904706943702026740316202794090470694318002263702376222477979226888950237625680406295620102406240400688013762686288012268889502376256804062956201024098884702475662

Try and solve it on your own with the test as a guide. Remember, when you see spikes in consistent intervals, that means “split up the text into groups of n (not transpose) and do something with these groups”.

Solving

Putting the text into the Kullback test, we clearly get spikes in intervals of two: 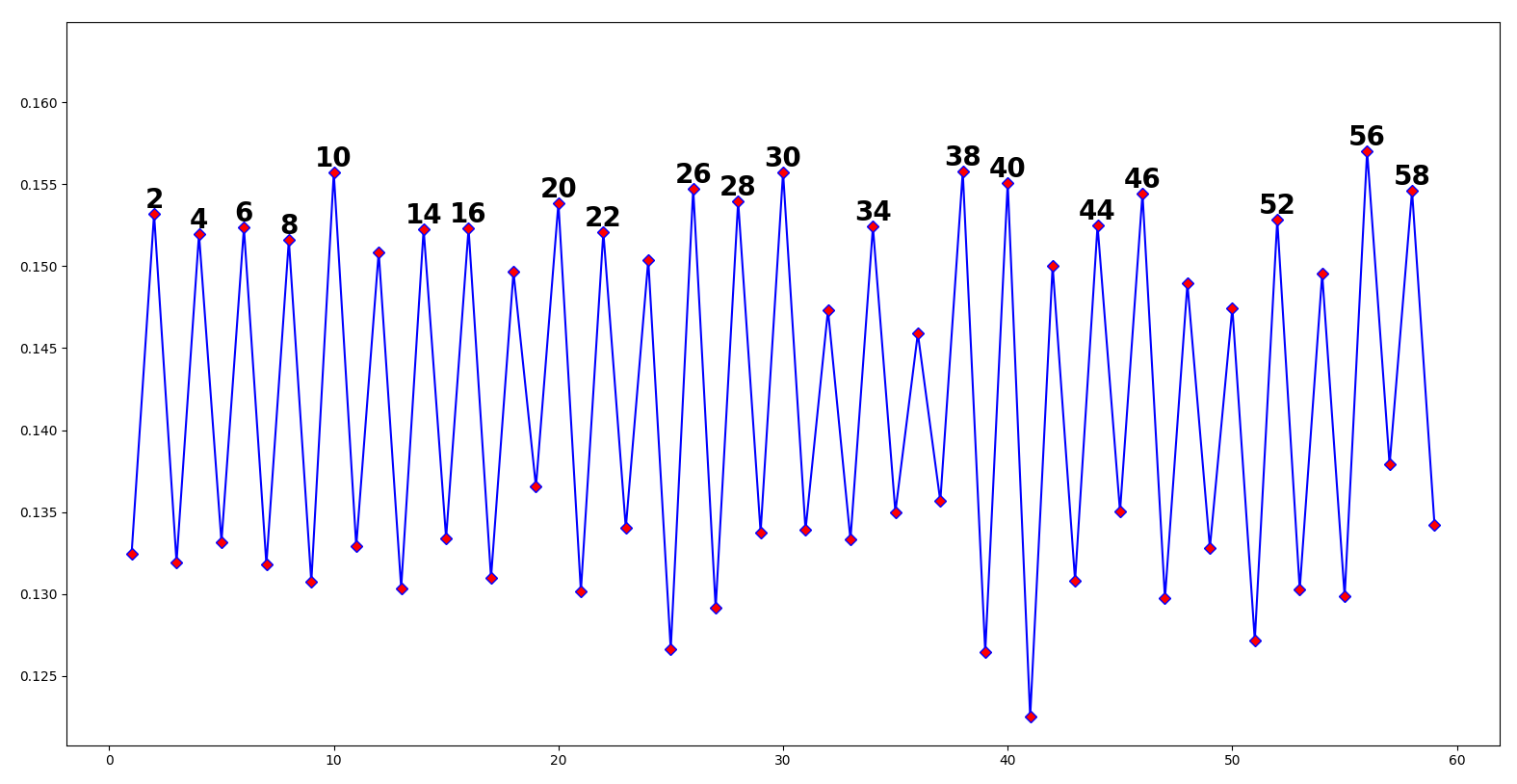So, let’s split our text into groups of two and see if we can find anything interesting. If I do so, and check how many unique groups of 2 come up, I get just 25: This is a very low number compared to the theoretical 100 possible groups of 2 we could get, and it’s also a number very close to 26. That heavily implies we’re dealing with a simple substitution cipher, where each letter in the alphabet has been replaced with a random 2-digit number. We can confirm this by assigning each unique group a letter (doable in dCode’s alphabetic transcription by setting the ngram size to 2) and putting it through a substitution cipher solver like quipqiup, giving us the solution!

Breaking a custom cipher in the wild

Instead of breaking a cipher I made, let’s break this cipher I came across on reddit with the Kullback test! Here’s the ciphertext:

0101001001100101011000010110110001101001011101000111100100100111011100110100011001100001011010110110010100101110010101010111000001101100011011110110000101100100010110010110111101110101011100100100110101101001011011100110010001001000011001010111001001100101010101000110111101000010011001010110011101101001011011100010111000000100000010000000100000010101010101010111011111110101010101001111110100000000101000011000001111000000010101111001111111000001010001011000011111110010110110100000101111011011001100001000001011011011010111010101101011110110100101110101101101001011101011110001000101011010111010010110100101110100110100101100101001011101001011011010000010010100001100110010100000101101101101111111010101010101010101011111110110110100000000001000101000100001000000000001011010010000010101011110100001011100111000101101100011110110100001101100110000111000110110110001101100100000110100000100010110011011010000011000110000111001000100111111000101101000110101001011111111110100011000100010110110010100011000001010001111101100111011011011011110110001001100111010011110101001101101000001010111011011000100001101111010010110100010110110100101001011011110110001001011011011011101100110011111110111100110101101101101110101011111101000101110011011010110110100000001010011111011100011010011100001011010011100010000100011000000000001101000101101101000010010010110111011011100110000110110110101011111011001111000010110010110011011010010101101101001000000001001111110100101101001100001001101101100110011111110110010110110000000001100111110111001100010111011011011011111110010000011010110110101011001101101001000001001111011000110011000111000010110100101110100100001000101000111111000001011011010111010001100101101011101011111101101101101011101000011110110100001001101110110110000100000100001000110001001010110100000011100011111110101011000110101011110001000011110000000000000000000000000000000000000001111100111110011001100010001100110011111001111100110001100110010001000100110011000110011100110010011001101000100010110011001001100100110001000110010100010001010011000100011000110011111001101010001000101011001111100110010010111010010101010101010101001011101001001010011100101010100111001010101001110010100100001110000101010001000101010000111000010011110101011110100000000000001111010101111000011010101100000111101111110001101010110001101001010010011110010000001110100101001011110101101101111000001000000011110110110101111010000001100001111111111100001110000010111101111011100111100001000011110001101111011110000111000110000011111000001100011100001111110011000110001111000111100011000110011111110011000110011100000000011100110001100111110011000001100000000000000000110000011011111011001110011000111101111000110011100100111001001101100111110000000111110011011011011101100100011001100001110000110011000100100100100110100110000100101001000011001011011010110010011001101111010101111011001100100100011011011110011100111111100111001111011011001001000001100000111101111000001100000101100100100011100010110011100110100010000010010010111111110111010000100001011101000111001101010011001110001011000001100011110010110010101001000001011100110101100101000000001001

Solving

When I initially stumbled upon this, my first guess was that this was ASCII text encoded as binary. If we try to decode it as such, we some output Reality'sFake.UploadYourMindHereToBegin but the rest seems complete gibberish: Now, let’s try throwing the binary into the Kullback test: 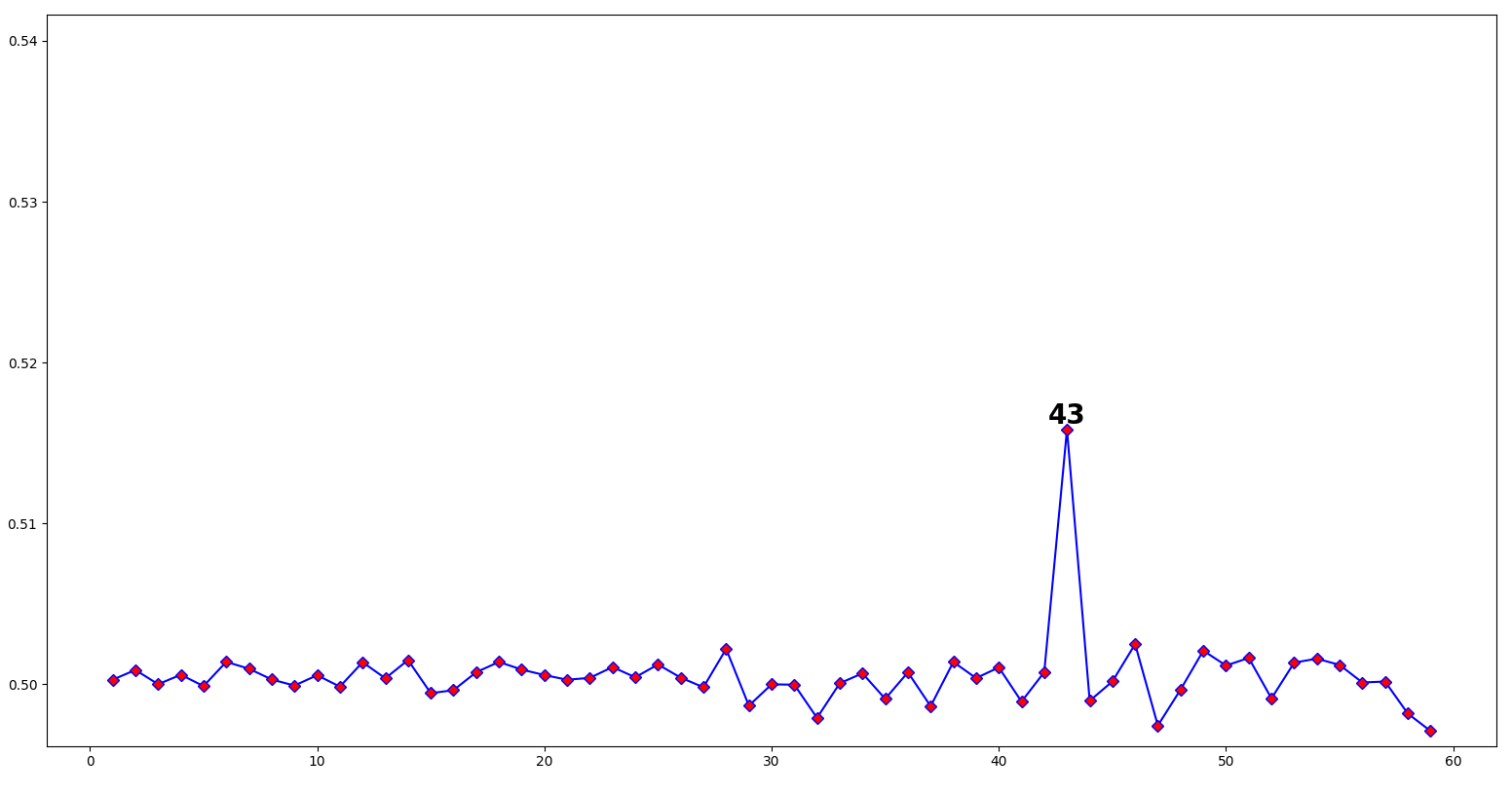Strange. We get absolutely nothing, and then a massive jump at 43. If I turn up the maxtest value in the script to check against higher values, we see the value is periodic: 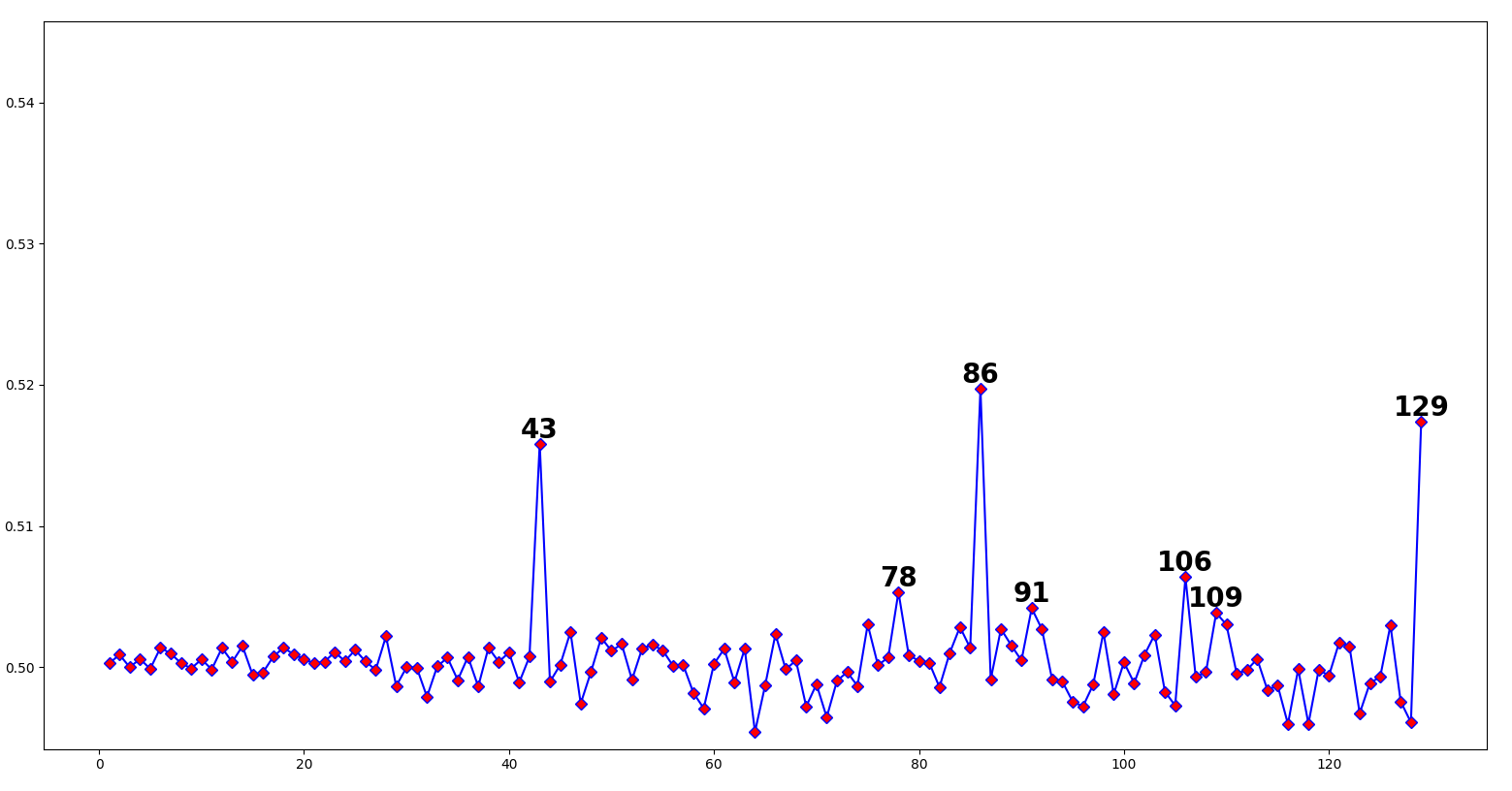With this in mind, let’s split the text into chunks of 43 and see if we notice anything: 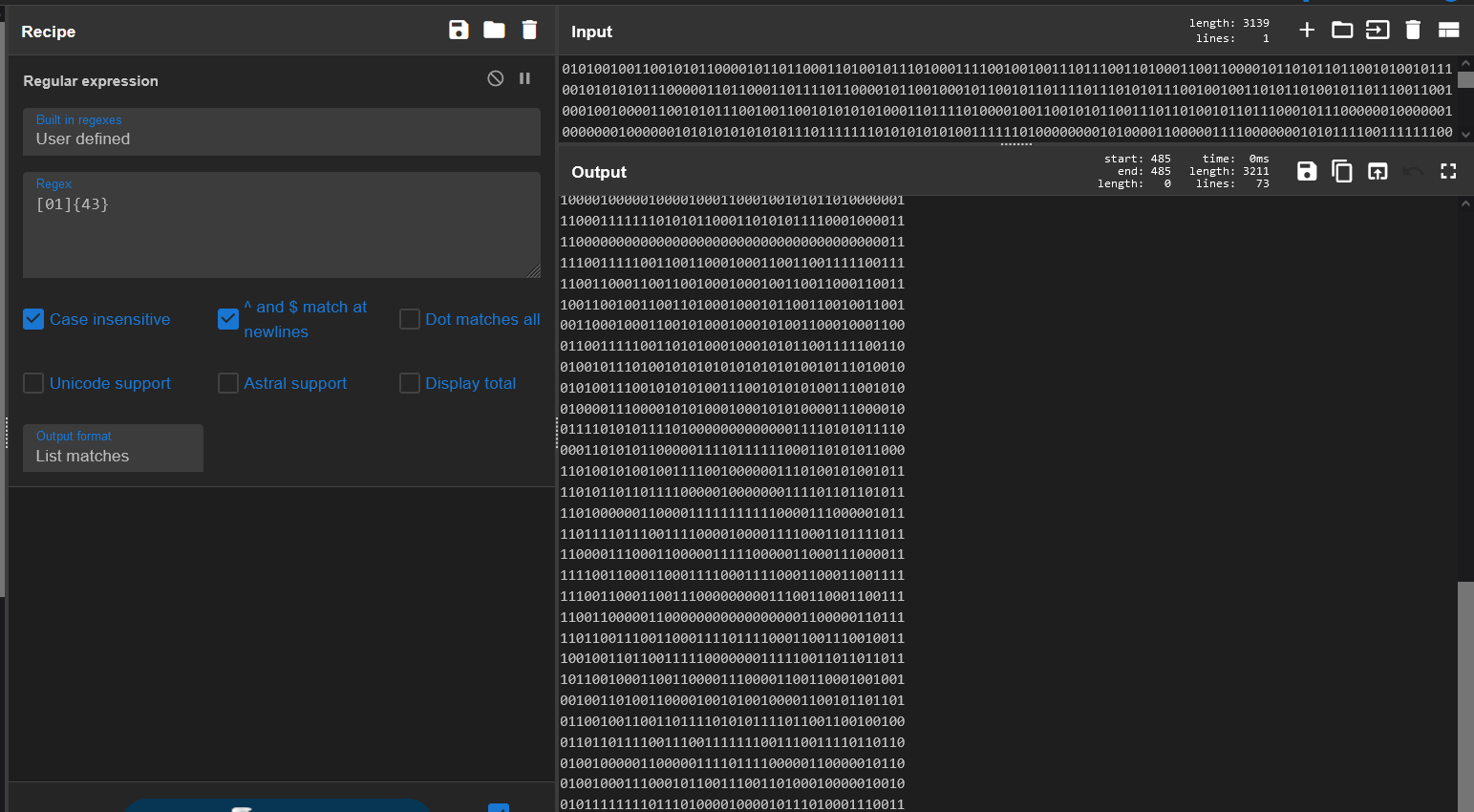It might be a little hard to see, but it looks like an image is being made out of 0’s and 1s. Let’s turn the 1’s into black pixels and the 0’s into white pixels: 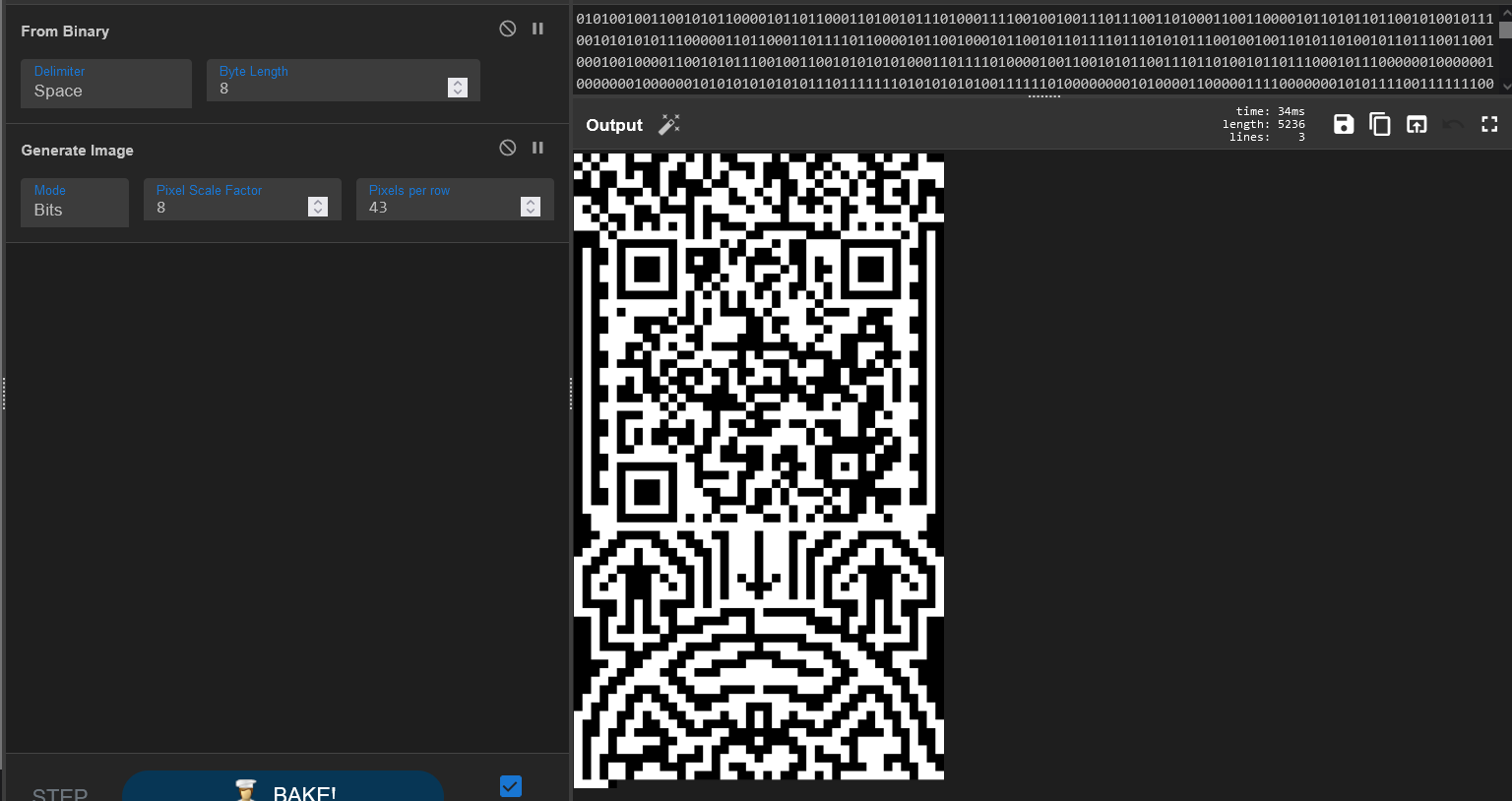Solved!

Solving a CTF Cipher

This one comes from a part in a maximum-point challenge during the PicoCTF 2023 competition, UnforgottenBits. The ciphertext is as follows:

01010010100.01001001000100.01001010000100.00101010010101.01000100100100.00100100000100.01000100000101.01000100001010.00000100000001.00001001010000.00000100010010.01000100010010.01001001001000.10001001000101.01001001010000.00001001000100.01001001010001.00000100000010.01000100010000.00001001001000.10000100010100.01000000010100.01001010000010.00101001010000.00001010101000.10000100100100.00101001000100.01000100010100.01001001010001.00000100010010.01000100010000.00001001000101.01000100010010.01000100010001.00000100001000.10001001000101.01001001001010.00000100010100.01000100000100.01000100010001.00000100000001.00000100001010.00000100010001.00001001000100.01000100000001.00000100001010.00000100001000.10000100000001.00000100010010.01001001001010.00000100000100.01000100010001.00000100001000.10001001010000.00001001010000.00000100000101.01001001000100.01000100010010.01000100010010.01001001000100.01000100010010.01000100000101.01001001000100.01001001001010.00000100010100.01000100010001.00000100000100.01000100000100.01000100000010.01000100010001.00001001000101.01000100010010.01000100000010.01001001010001.00001001001010.00001001001000.10000100000100.01001001000101.01001001000101.01000100010010.01001001010000.00000100010010.01001001001000.10001001000100.01000100010010.01000100010001.00000100000101.01000100010000.00001001001010.00001001000100.01000000010100.01001001010101.01001010100010.00100100100100.00100100010100.01000100000001.00000100010010.01000100001000.10000100001010.00000100010010.01001001010000.00000100001000.10000100010010.01001001010001.00001001001000.10000100010010.01001001001010.00001001000101.01000100000010.01001001001000.10000100001010.00001001000100.01000100001000.10000100010000.00001001010001.00000100000010.01000100010010.01001001010001.00000100000001.00001001010001.00001001010000.00001001000101.01000100000010.01000100000010.01000100010100.01001001010001.00000000010100.010

In a previous section, you were hinted at using this website.

Solving

Again, let’s put it through the Kullback test: 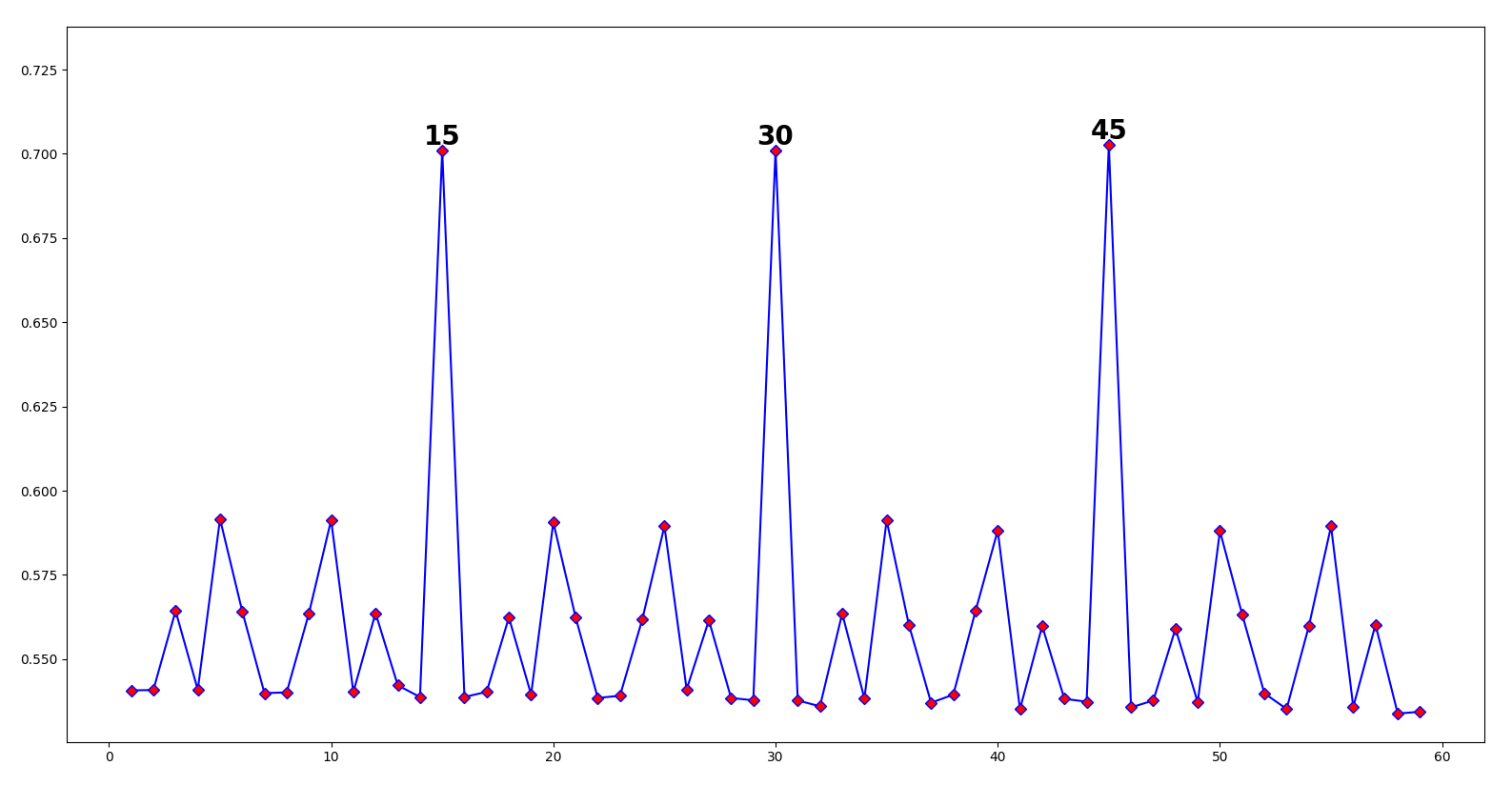Highly periodic at 15! So, let’s split up our text into chunks of 15:

01010010100.010
01001000100.010
01010000100.001
01010010101.010
00100100100.001
00100000100.010
00100000101.010
00100001010.000
00100000001.000
01001010000.000
00100010010.010
00100010010.010
01001001000.100
01001000101.010
01001010000.000
01001000100.010
01001010001.000
00100000010.010
00100010000.000
01001001000.100
...

If we put each number through the Phigits calculator I linked, we get numbers that are all close to ASCII decimal. Rounding each number and decoding it as ASCII decimal gives us instructions on how to decrypt a piece of data in the challenge!

Final Words and Footguns

Hopefully you can see where the Kullback test can help out. It easily helps you find where text starts to repeat on itself, giving you a hint to split the text into groups and do an operation on each individual group. As a bonus, here’s a few more interesting things that show up as periodic with this test:

• Base64-encoded nonrandom text is periodic by 4: 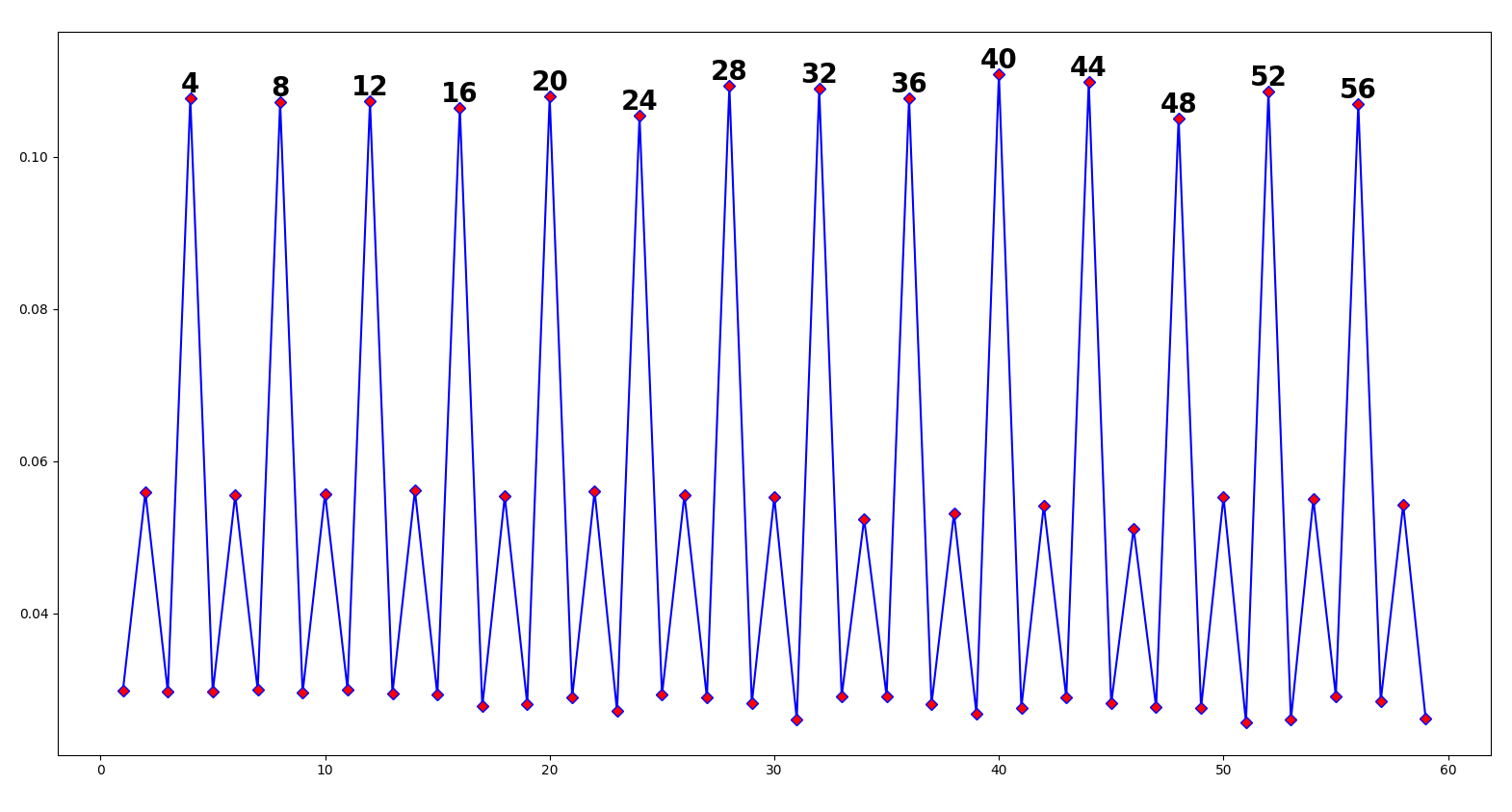This is because 3 input characters get substituted for 4 base64 characters.
• Binary-encoded nonrandom text is periodic by 8: 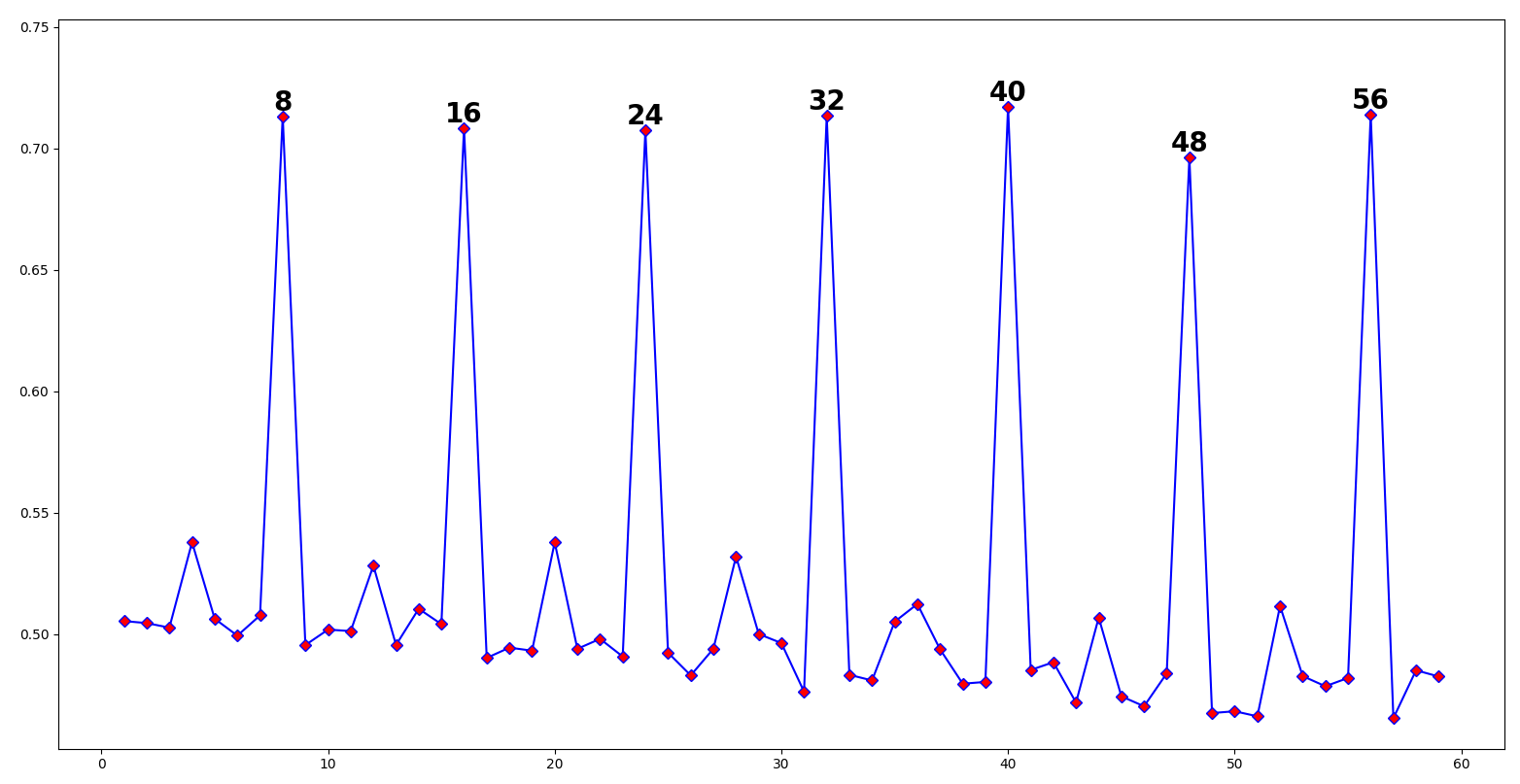As you might guess, this is because text gets commonly encoded into 8 bits.
• Code written in the Malbolge programming language is periodic by 94: 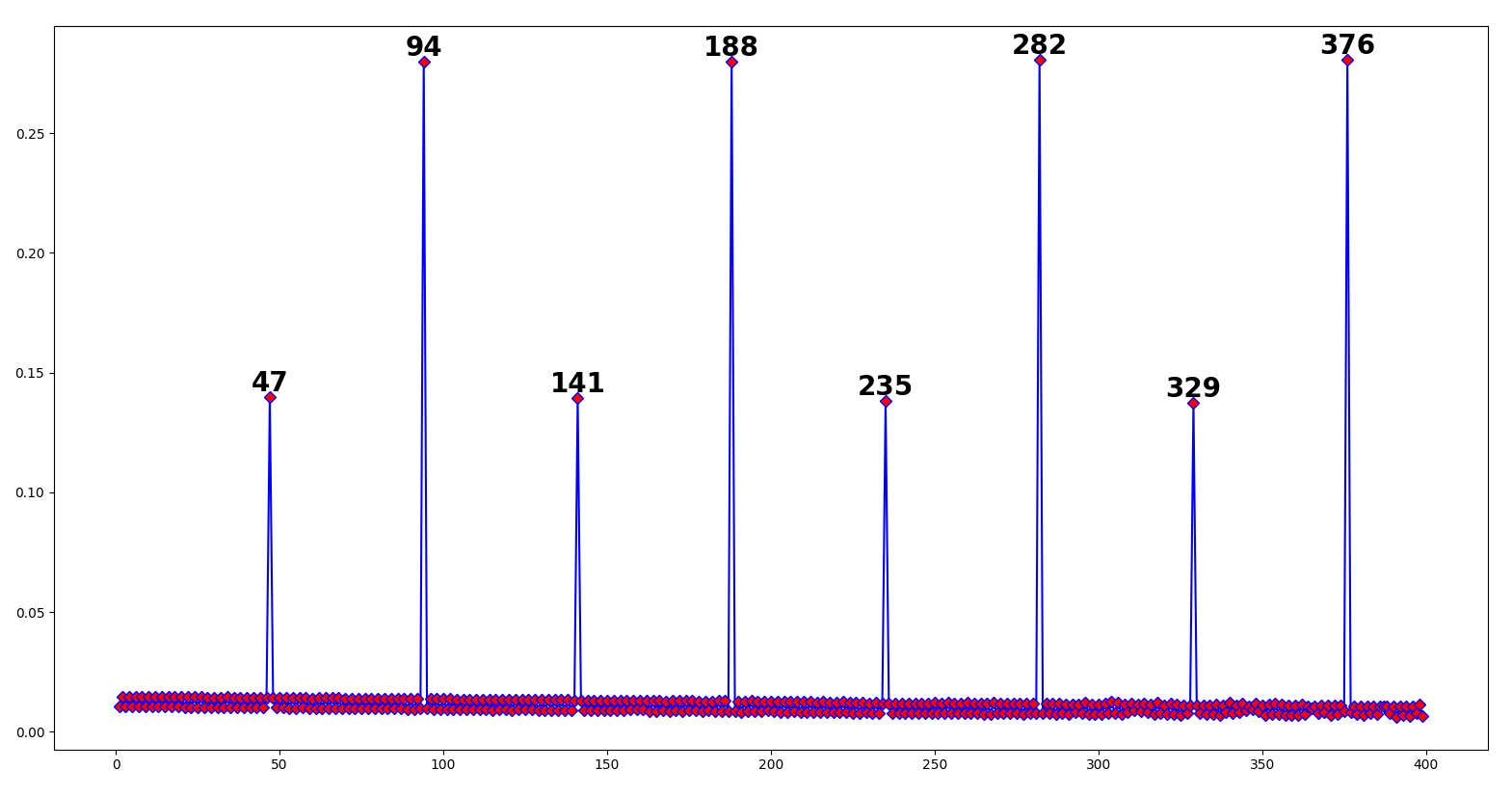This is because Malbolge works under modulo 94.

Of course, not everything is periodic, and you need to know what this looks like. For instance, regular plaintext is very much not: 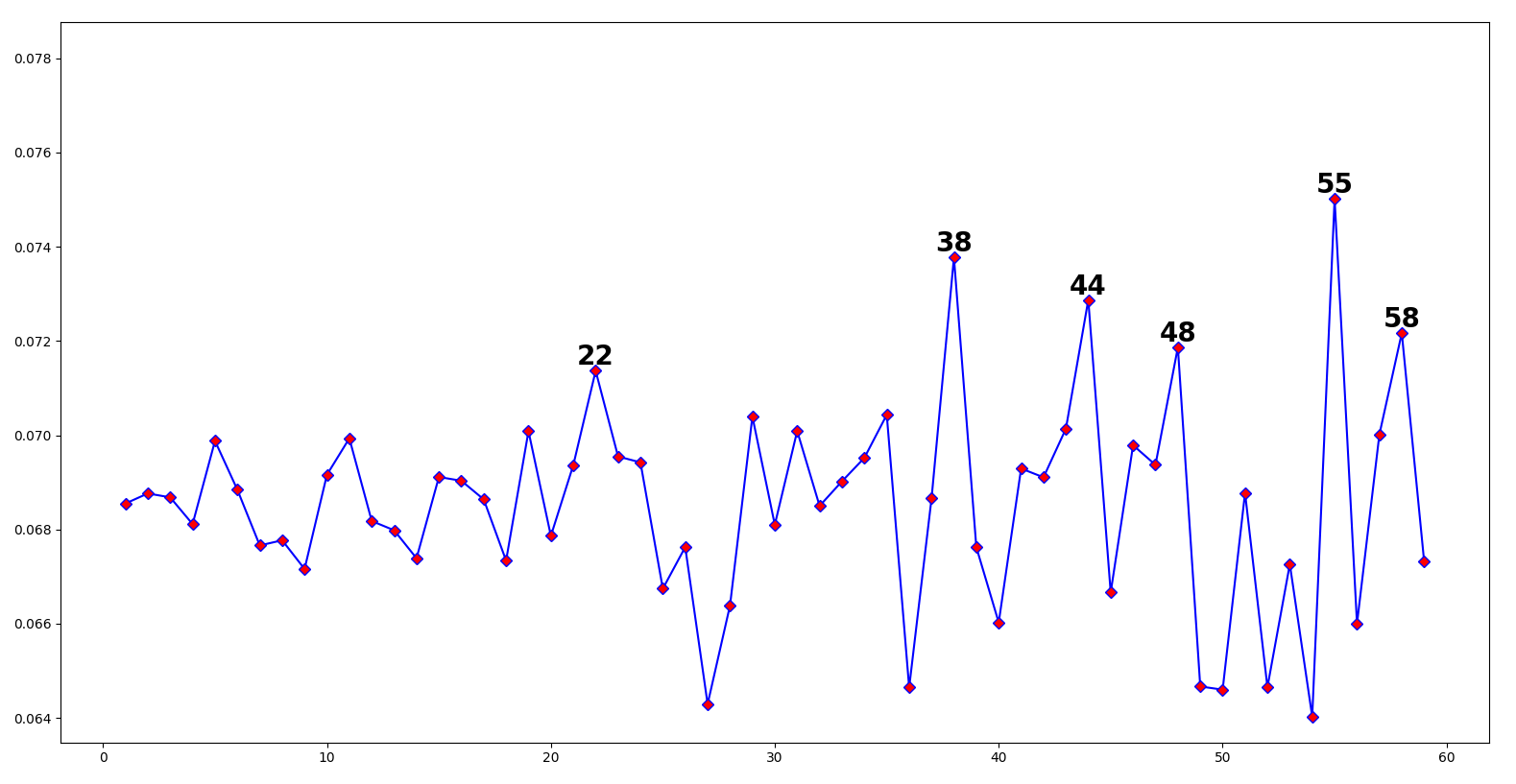There are spikes, but they’re clearly not periodic in any way. Keep this in mind if you’re going to use this program; if you don’t see spikes repeating in consistent intervals, ignore it.